Contents

1 Download
3 Algoritmos
3.1 Búsqueda de extremos
3.1.1 Hallar el punto con mayor abscisa.
3.1.2 Dada un vector, hallar el extremo según la dirección de ese vector.
3.1.3 Hallar el rectángulo mínimo de lados paralelos a los ejes que contiene a todos los puntos.
3.2 Ordenaciones
3.2.1 Ordenar los puntos segun sus abscisas de menor a mayor.
3.2.2 Ordenar los puntos según una dirección dada por un vector.
3.2.3 Ordenar los puntos angularmente respecto de un punto dado y en sentido positivo, comenzando por el de menor ordenada.
3.3 Búsqueda en rangos
3.3.1 Escribir un algoritmo que calcule, para cada rectángulo de lados paralelos a los ejes, el número de puntos del conjunto que contiene.

Download

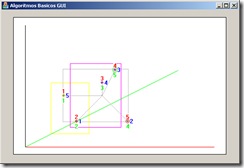
Aplicación sencillo demostrando el uso de los algoritmos siguientes

• Proyecto Visual Studio 2005 (C++)

Captura de pantalla

Algoritmos

Búsqueda de extremos

Hallar el punto con mayor abscisa.

int MaximumAbscissa(std::vector<Point2D> * pvPoints, Point2D * pptResult)
{
	if(pvPoints->size() == 0)
		return 0;

	bool bDoubles = false;

	Point2D ptTemp = (*pvPoints)[0];
	for(unsigned int i = 1; i < pvPoints->size(); i++){
		if((*pvPoints)[i].x > ptTemp.x){
			ptTemp = (*pvPoints)[i];
			bDoubles = false;
		}
		else if((*pvPoints)[i].x == ptTemp.x)
			bDoubles = true;
	}

	*pptResult = ptTemp;

	if(bDoubles)
		return 2;
	else
		return 1;
}

bool MaximumAbscissaMultiple(std::vector<Point2D> * pvPoints, std::vector<Point2D> * pvResult)
{
	pvResult->clear();

	Point2D ptTemp;
	int iResult = MaximumAbscissa(pvPoints, &ptTemp);
	if(iResult == 0)
		return false;
	else if(iResult == 1){
		pvResult->push_back(ptTemp);
		return true;
	}
	else{
		for(unsigned int i = 0; i < pvPoints->size(); i++){
			if((*pvPoints)[i].x == ptTemp.x)
				pvResult->push_back((*pvPoints)[i]);
			return true;
		}
		return false;
	}
}

Dada un vector, hallar el extremo según la dirección de ese vector.

int MaximumInDirection(std::vector<Point2D> * pvPoints, Point2D ptDireccion, Point2D * pptResult)
{
	if(pvPoints->size() == 0)
		return 0;

	bool bDoubles = false;

	Point2D ptTemp = (*pvPoints)[0];
	float fLength = (*pvPoints)[0] * ptDireccion;
	for(unsigned int i = 1; i < pvPoints->size(); i++){
		if(fLength < (*pvPoints)[i] * ptTemp){
			ptTemp = (*pvPoints)[i];
			fLength = (*pvPoints)[i] * ptTemp;
			bDoubles = false;
		}
		else if(fLength == (*pvPoints)[i] * ptTemp)
			bDoubles = true;
	}

	*pptResult = ptTemp;

	if(bDoubles)
		return 2;
	else
		return 1;
}

Hallar el rectángulo mínimo de lados paralelos a los ejes que contiene a todos los puntos.

bool BoundingBox(std::vector<Point2D> * pvPoints, Rect2D * prctResult)
{
	if(pvPoints->size() == 0)
		return false;

	Point2D ptLeftBottom, ptUpperRight;
	ptLeftBottom = ptUpperRight = (*pvPoints)[0];
	for(unsigned int i = 1; i < pvPoints->size(); i++){
		ptLeftBottom = min(ptLeftBottom, (*pvPoints)[i]);
		ptUpperRight = max(ptUpperRight, (*pvPoints)[i]);
	}

	*prctResult = Rect2D(ptLeftBottom, ptUpperRight);
	return true;
}

Ordenaciones

Ordenar los puntos segun sus abscisas de menor a mayor.

void SortPointsByAbscissaAscending(std::vector<Point2D> * pvPoints, std::vector<Point2D> * pvResult)
{
	pvResult->clear();

	pvResult->insert(pvResult->begin(), pvPoints->begin(), pvPoints->end());
	std::sort(pvResult->begin(), pvResult->end(), SortAbscissaAsc);
}

bool SortAbscissaAsc(Point2D ptPoint1, Point2D ptPoint2)
{
	return ptPoint1.x < ptPoint2.x;
}

Ordenar los puntos según una dirección dada por un vector.

void SortPointsByDirectionAscending(std::vector<Point2D> * pvPoints, Point2D ptDireccion, std::vector<Point2D> * pvResult)
{
	pvResult->clear();

	std::vector<SPOINTWITHDIRECTION> vTemp;

	SPOINTWITHDIRECTION spwdPointTemp;
	for(unsigned int i = 0; i < pvPoints->size(); i++){
		spwdPointTemp.ptPoint = (*pvPoints)[i];
		spwdPointTemp.fProjection = spwdPointTemp.ptPoint * ptDireccion;
		vTemp.push_back(spwdPointTemp);
	}

	std::sort(vTemp.begin(), vTemp.end(), SortDirectionAsc);

	for(unsigned int i = 0; i < vTemp.size(); i++)
		pvResult->push_back(vTemp[i].ptPoint);
}

bool SortDirectionAsc(SPOINTWITHDIRECTION ptPoint1, SPOINTWITHDIRECTION ptPoint2)
{
	return ptPoint1.fProjection < ptPoint2.fProjection;
}

Ordenar los puntos angularmente respecto de un punto dado y en sentido positivo, comenzando por el de menor ordenada.

void SortPointsAngular(std::vector<Point2D> * pvPoints, Point2D ptRef, std::vector<Point2D> * pvResult)
{
	pvResult->clear();
	if(pvPoints->size() == 0)
		return;

	std::vector<SPOINTWITHDIRECTION> vPointsQ1, vPointsQ2, vPointsQ3, vPointsQ4;

	for(unsigned int i = 0; i < pvPoints->size(); i++){
		Point2D ptTemp = (*pvPoints)[i];
		SPOINTWITHDIRECTION spwdTemp;
		spwdTemp.ptPoint = ptTemp;
		spwdTemp.fProjection = abs(ptTemp.x - ptRef.x);

		if(ptTemp.x >= ptRef.x){
			if(ptTemp.y <= ptRef.y)
				vPointsQ1.push_back(spwdTemp);
			else
				vPointsQ2.push_back(spwdTemp);
		}
		else{
			if(ptTemp.y >= ptRef.y)
				vPointsQ3.push_back(spwdTemp);
			else
				vPointsQ4.push_back(spwdTemp);
		}
	}

	std::sort(vPointsQ1.begin(), vPointsQ1.end(), SortDirectionAsc);
	std::sort(vPointsQ2.begin(), vPointsQ2.end(), SortDirectionDesc);
	std::sort(vPointsQ3.begin(), vPointsQ3.end(), SortDirectionAsc);
	std::sort(vPointsQ4.begin(), vPointsQ4.end(), SortDirectionDesc);

	std::vector<SPOINTWITHDIRECTION> vJoin;

	vJoin.insert(vJoin.end(), vPointsQ1.begin(), vPointsQ1.end());
	vJoin.insert(vJoin.end(), vPointsQ2.begin(), vPointsQ2.end());
	vJoin.insert(vJoin.end(), vPointsQ3.begin(), vPointsQ3.end());
	vJoin.insert(vJoin.end(), vPointsQ4.begin(), vPointsQ4.end());

	int iIndex = 0;
	float fMinOrd = vJoin[0].ptPoint.y;
	for(unsigned int i = 1; i < vJoin.size(); i++){
		if(vJoin[i].ptPoint.y <= fMinOrd){
			fMinOrd = vJoin[i].ptPoint.y;
			iIndex = i;
		}
	}

	for(unsigned int i = iIndex; i < vJoin.size(); i++)
		pvResult->push_back(vJoin[i].ptPoint);

	for(unsigned int i = 0; i < iIndex; i++)
		pvResult->push_back(vJoin[i].ptPoint);
}

bool SortDirectionDesc(SPOINTWITHDIRECTION ptPoint1, SPOINTWITHDIRECTION ptPoint2)
{
	return ptPoint1.fProjection > ptPoint2.fProjection;
}

Búsqueda en rangos

Escribir un algoritmo que calcule, para cada rectángulo de lados paralelos a los ejes, el número de puntos del conjunto que contiene.

void PointsInRect(std::vector<Point2D> * pvPoints, Rect2D rcFrame, std::vector<Point2D> * pvResult)
{
	pvResult->clear();

	for(unsigned int i = 0; i < pvPoints->size(); i++){
		Point2D ptTemp = (*pvPoints)[i];
		if(ptTemp.x >= rcFrame.ptLeftBottom.x && ptTemp.y >= rcFrame.ptLeftBottom.y && ptTemp.x <= rcFrame.ptUpperRight.x && ptTemp.y <= rcFrame.ptUpperRight.y)
			pvResult->push_back(ptTemp);
	}
}